フィボナッチヒープ - 宇宙ツイッタラーXの憂鬱

フィボナッチヒープとは

この記事ではヒープは最小値を求めるものとします。

フィボナッチヒープとは、フィボナッチ数の性質をうまく使ってならし計算量で高い性能を持ったヒープです。

ヒープ	フィボナッチヒープ	二分ヒープ
最小値の削除	ならし O(log n)	O(log n)
値の追加	O(1)	O(log n)

値の追加が非常に多く、最小値の削除が非常に少ない場合は、二分ヒープより速くなることもあるかもしれません。他にもヒープ同士をマージできたり、ヒープ内の値の減少ができたりしますが、この記事では扱いません。すみません。

構造

図は wikipedia からの引用です。

フィボナッチヒープは、下図のようにいくつかのツリーを並べたような構造を持っています。ツリーの各ノードに、ヒープ内の値が入っています。各ツリーでは、上の根に近いほうが小さい値になるようになっています。このとき、ヒープ内の値の最小値は 1 で、実際に最小値のポインタも 1 のノードを指しています。

f:id:kenkoooo:20171201145535p:plain

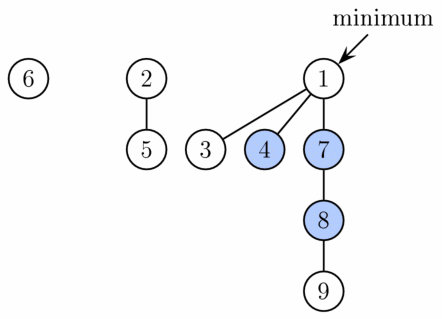
次に、最小値を削除 (pop) することを考えます。先ほど最小値とされていた 1 のノードが削除され、1 を根としたツリーが分解し、新たに 3, 4, 7 をそれぞれ根とした新しいツリーができます。新しいツリーたちはヒープのツリーのリストに入ります。

f:id:kenkoooo:20171201150203p:plain

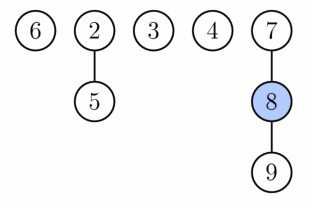
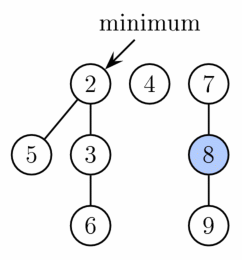
今度はツリーのリストを整理します。ツリーを順番に見ていき、以下の操作を施します。

見ているツリーの根の次数を i とする。

次数 i のツリーとして登録されているツリーが他になければ、今見ているツリーを次数 i のツリーとして登録する。
次数 i のツリーとして登録されているツリーが既にある場合、登録されているツリーの根の値と、今見ているツリーの根の値を比べ、大きい方の根を小さい方の根の下に接続する。この操作で次数 i の根を持ったツリーが 2 つ消え、次数 i+1 を持ったツリーが新たに生成される。

この操作を全て終えると、ヒープ内のツリーの根の次数が全て相異なるようになります。（後述しますが、これは重要なことです）
最後に残っているツリーの根をもう一度全て見て、最小の値を持つ根を最小値として指すようにします。

f:id:kenkoooo:20171201150551p:plain

計算量

ツリーのリストを走査するときにノードを参照する回数は、新たに追加されたノードの数 + 最小値のノードの子ノードの数であるが、新たに追加されたノードの数はノードを追加する計算量に含めるとして、最小値のノードの子ノードの数、すなわち最小値のノードの次数が $O(\log n)$ となることを示す。

補題 1

あるノード x について、 x の次数を $x.degree$ と表す。 $x.degree=k$ として、x の k 個の子ノードをそれぞれ $y_1, y_2, y_3, ..., y_k$ として、この順番で x の子として接続されたとする。この時 $y_1.degree \geq 0$ かつ $y_i.degree \geq i - 2 (i=2,3,...,k)$ である。

証明

$y_1.degree \geq 0$ は自明。

$i \geq 2$ に対して $y_i$ を x に接続する時、 $y_1, ... , y_{i-1}$ は既に x の子ノードとして接続されている。つまり $x.degree \geq i-1$ が成り立っている。
ここで $y_i$ が x に子として接続されるためには $x.degree= y_i.degree$ が成り立っていなければならない。よって $y_i.degree \geq i-1$ が成り立つ。
値が減少するバージョンではまだやることがありますが、とりあえずこれで $y_i.degree \geq i-2$ が成り立ったのでこのまま行きます。

補題 2

k 番目のフィボナッチ数を $F_k$ と表す。この時 $F_0=0, F_1=1$ とする。k (k > 2) 番目のフィボナッチ数 $F_k$ の漸化式は $F_k=F_{k-1}+F_{k-2}$ である。

この時、任意の $k \geq 0$ について $F_{k+2} = 1 + \sum^{k}_{i=0} F_i$ が成り立つ。

証明

帰納法で示す。

k=0 のとき成り立つ。

$F_{k+1} = 1 + \sum^{k-1}_{i=0}F_i$ が成り立つことを仮定すると、 $F_{k+2}=F_{k+1}+F_k=F_k+1+ \sum^{k-1}_{i=0}F_i = 1 + \sum^{k}_{i=0} F_i$

補題 3

$\phi$ を $x^2-x-1=0$ の正の解とする。

全ての整数 $k \geq 0$ に対して、 k+2 番目のフィボナッチ数 $F_{k+2}$ は $F_{k+2} \geq \phi^k$ を満たす。

証明

帰納法で示す。

$k=0$ のとき $F_2=1=\phi^0$
$k=1$ のとき $F_3=2>\phi^1$

$F_i + 2 > \phi^i (i=0,1,2,...,k-1)$ を仮定すると $F_{k+2} = F_{k+1} +F_k \geq \phi^{k-1} + \phi^{k-2} = \phi^{k-2}(\phi + 1) = \phi^{k-2} \phi^2 = \phi^k$

補題 4

ノード x について $x.degree=k$ とする。 $size(x)$ を、ノード x を根とする部分木の頂点数とすると、 $size(x) \geq \phi^k$ が成り立つ。

証明

次数 k のあるノード z の $size(z)$ が取りうる最小値を $s_k$ とする。 $s_0=1, s_1=2$ である。また、 $s_k$ は k について単調増加である。z の k 個の子ノードを $y_1, ... , y_k$ とすると、

$size(z) \geq s_k \geq 2 + \sum^{k}_{i=2} s_{y_i.degree} \geq 2 + \sum^{k}_{i=2}s_{i-2}$

(補題 1 より $y_i.degree \geq i-2$ であり、 $s_k$ は単調増加なので $s_{y_i.degree} \geq s_{i-2}$ である)

$s_i \geq F_{i+2} (i=0,1,2,... ,K-1)$ を仮定すると $s_k \geq 2 + \sum^{k}_{i=2}s_{i-2} \geq 2 +\sum^{k}_{i=2}F_{i} = 1 + \sum^{k}_{i=0}F_i = F_{k+2 } \geq \phi^k$

よって $size(x) \geq s_k \geq F_{k+2} \geq \phi^k$

系 5

要素数 n のフィボナッチヒープに属する任意の頂点の最大次数 $D(n)$ は $O(\log n)$ である。

証明

要素数 n のフィボナッチヒープの任意のノードを x とし、 $k = x.degree$ とする。
$n \geq size(x) \geq \phi^k$ だから $\log_{\phi}n \geq k$

よって任意の頂点の次数は $\log_{\phi}n$ で抑えられる。

実装

import java.util.ArrayList;
import java.util.List;

public class LongFibonacciHeap {

  class Node {

    long key = -1;
    int degree = 0;
    Node p = null;
    Node right = null;
    Node left = null;
    List<Node> children = new ArrayList<>();
    boolean mark = false;
  }

  private Node min = null;
  private int size = 0;

  public void insert(Node x) {
    if (min == null) {
      min = x;
      x.right = x;
      x.left = x;
    } else {
      addRoot(x);
      if (x.key < min.key) {
        min = x;
      }
    }
    size++;
  }

  /**
   * Add node x to linked root list
   *
   * @param x node to add
   */
  private void addRoot(Node x) {
    if (min == null) {
      min = x;
      min.right = x;
      min.left = x;
      return;
    }

    Node l = min.left;
    l.right = x;
    min.left = x;

    x.right = min;
    x.left = l;
  }

  /**
   * Remove node x from linked root list
   *
   * @param x node to remove
   */
  private void removeRoot(Node x) {
    Node r = x.right;
    Node l = x.left;
    r.left = l;
    l.right = r;
  }

  /**
   * merge h1 and h2 to generate new one
   *
   * @param h1 heap1 to merge
   * @param h2 heap2 to merge
   * @return merged heap
   */
  public static LongFibonacciHeap unite(LongFibonacciHeap h1, LongFibonacciHeap h2) {
    LongFibonacciHeap h = new LongFibonacciHeap();
    h.min = h1.min;
    if ((h1.min == null) || (h2.min != null && h2.min.key < h1.min.key)) {
      h.min = h2.min;
    }

    // link h1's root list & h2's root list
    if (h1.min != null && h2.min != null) {
      Node n1 = h1.min;
      Node n2 = h2.min;
      Node n1l = n1.left;
      Node n2r = n2.right;

      n1.left = n2;
      n2.right = n1;
      n2r.left = n1l;
      n1l.right = n2r;
    }

    h.size = h1.size + h2.size;
    return h;
  }

  public Node extractMinNode() {
    Node z = min;
    if (z == null) {
      return null;
    }

    for (Node child : z.children) {
      addRoot(child);
      child.p = null;
    }
    removeRoot(z);
    if (z == z.right) {
      min = null;
    } else {
      min = z.right;
      consolidate();
    }
    size--;
    return z;
  }

  public int size() {
    return size;
  }

  private void consolidate() {
    //list up rooted nodes
    ArrayList<Node> rootList = new ArrayList<>();
    rootList.add(min);
    while (rootList.get(rootList.size() - 1).right != rootList.get(0)) {
      Node lastRight = rootList.get(rootList.size() - 1).right;
      rootList.add(lastRight);
    }

    Node[] rootOfDegree = new Node[size + 1];
    for (Node parent : rootList) {
      int d = parent.degree;
      while (rootOfDegree[d] != null) {
        Node child = rootOfDegree[d];
        if (parent.key > child.key) {
          Node t = parent;
          parent = child;
          child = t;
        }
        link(child, parent);
        rootOfDegree[d] = null;
        d++;
      }
      rootOfDegree[d] = parent;
    }

    min = null;
    for (Node node : rootOfDegree) {
      if (node == null) {
        continue;
      }

      if (min == null) {
        node.right = node;
        node.left = node;
        min = node;
      } else {
        addRoot(node);
        if (node.key < min.key) {
          min = node;
        }
      }
    }
  }

  private void link(Node child, Node parent) {
    removeRoot(child);
    parent.degree++;
    parent.children.add(child);
    child.p = parent;
    child.mark = false;
  }

  public void insert(long key) {
    Node x = new Node();
    x.key = key;
    insert(x);
  }
}

フィボナッチヒープを使ってダイクストラやってみた

問題

atcoder.jp

コード

use std::cmp;
use std::collections::HashMap;

const INF: u64 = std::u64::MAX / 2;

fn main() {
    let s = std::io::stdin();
    let mut sc = Scanner { stdin: s.lock() };
    let n: usize = sc.read();
    let m: usize = sc.read();
    let s = sc.read::<usize>() - 1;
    let t = sc.read::<usize>() - 1;

    let mut graph = vec![vec![]; n];
    for _ in 0..m {
        let a = sc.read::<usize>() - 1;
        let b = sc.read::<usize>() - 1;
        let c = sc.read::<u64>();
        graph[a].push((b, c));
        graph[b].push((a, c));
    }

    let dist1 = dijkstra(s, &graph);
    let dist2 = dijkstra(t, &graph);
    for i in 0..n {
        if dist1[i] == dist2[i] && dist1[i] != INF {
            println!("{}", i + 1);
            return;
        }
    }
    println!("-1");
}

fn dijkstra(s: usize, graph: &Vec<Vec<(usize, u64)>>) -> Vec<u64> {
    let n = graph.len();
    let mut dist = vec![INF; n];
    dist[s] = 0;
    let mut heap = FibonacciHeap::new(cmp::min);
    heap.push((0, s));
    while let Some((_, v)) = heap.pop() {
        for &(next, cost) in graph[v].iter() {
            if dist[next] > dist[v] + cost {
                dist[next] = dist[v] + cost;
                heap.push((dist[next], next));
            }
        }
    }
    dist
}

fn store_to_map<T, F>(map: &mut HashMap<usize, Node<T>>, mut node: Node<T>, ordering: F)
where
    T: Copy + PartialEq,
    F: Fn(T, T) -> T,
{
    let d = node.children.len();
    match map.remove(&d) {
        Some(mut other) => {
            let node = if (ordering)(node.key, other.key) == node.key {
                node.children.push(other);
                node
            } else {
                other.children.push(node);
                other
            };
            store_to_map(map, node, ordering);
        }
        None => {
            map.insert(d, node);
        }
    }
}

pub struct FibonacciHeap<T, F> {
    pub nodes: Vec<Node<T>>,
    min_index: usize,
    ordering: F,
}

impl<T, F> FibonacciHeap<T, F>
where
    T: Copy + PartialEq,
    F: Fn(T, T) -> T + Copy,
{
    pub fn new(ordering: F) -> FibonacciHeap<T, F> {
        FibonacciHeap {
            nodes: Vec::new(),
            min_index: 0,
            ordering: ordering,
        }
    }
    pub fn push(&mut self, x: T) {
        let node = Node::new(x);
        self.nodes.push(node);
        let cur_min = self.nodes[self.min_index].key;
        if (self.ordering)(cur_min, x) == x {
            self.min_index = self.nodes.len() - 1;
        }
    }
    pub fn pop(&mut self) -> Option<T> {
        let mut map: HashMap<usize, Node<T>> = HashMap::new();
        let mut popped = None;

        let mut nodes = Vec::new();
        std::mem::swap(&mut self.nodes, &mut nodes);
        for (i, node) in nodes.into_iter().enumerate() {
            if i == self.min_index {
                popped = Some(node.key);
                for node in node.children.into_iter() {
                    store_to_map(&mut map, node, self.ordering);
                }
            } else {
                store_to_map(&mut map, node, self.ordering);
            }
        }

        self.nodes = map.into_iter().map(|(_, node)| node).collect();
        if !self.nodes.is_empty() {
            let mut min = self.nodes[0].key;
            for i in 0..self.nodes.len() {
                if (self.ordering)(min, self.nodes[i].key) == self.nodes[i].key {
                    min = self.nodes[i].key;
                }
            }

            self.min_index = self
                .nodes
                .iter()
                .enumerate()
                .find(|&(_, node)| node.key == min)
                .unwrap()
                .0;
        } else {
            self.min_index = 0;
        }
        popped
    }
}

#[derive(Debug)]
pub struct Node<T> {
    pub key: T,
    pub children: Vec<Node<T>>,
}

impl<T> Node<T> {
    fn new(x: T) -> Node<T> {
        Node {
            key: x,
            children: Vec::new(),
        }
    }
}

pub struct Scanner<R> {
    stdin: R,
}

impl<R: std::io::Read> Scanner<R> {
    pub fn read<T: std::str::FromStr>(&mut self) -> T {
        use std::io::Read;
        let buf = self
            .stdin
            .by_ref()
            .bytes()
            .map(|b| b.unwrap())
            .skip_while(|&b| b == b' ' || b == b'\n')
            .take_while(|&b| b != b' ' && b != b'\n')
            .collect::<Vec<_>>();
        unsafe { std::str::from_utf8_unchecked(&buf) }
            .parse()
            .ok()
            .expect("Parse error.")
    }
    pub fn vec<T: std::str::FromStr>(&mut self, n: usize) -> Vec<T> {
        (0..n).map(|_| self.read()).collect()
    }
    pub fn chars(&mut self) -> Vec<char> {
        self.read::<String>().chars().collect()
    }
}