2017-12-01

フィボナッチヒープ

フィボナッチヒープとは

この記事ではヒープは最小値を求めるものとします。

フィボナッチヒープとは、フィボナッチ数の性質をうまく使ってならし計算量で高い性能を持ったヒープです。

ヒープ	フィボナッチヒープ	二分ヒープ
最小値の削除	ならし O(log n)	O(log n)
値の追加	O(1)	O(log n)

値の追加が非常に多く、最小値の削除が非常に少ない場合は、二分ヒープより速くなることもあるかもしれません。他にもヒープ同士をマージできたり、ヒープ内の値の減少ができたりしますが、この記事では扱いません。すみません。

構造

図は wikipedia からの引用です。

フィボナッチヒープは、下図のようにいくつかのツリーを並べたような構造を持っています。ツリーの各ノードに、ヒープ内の値が入っています。各ツリーでは、上の根に近いほうが小さい値になるようになっています。このとき、ヒープ内の値の最小値は 1 で、実際に最小値のポインタも 1 のノードを指しています。

f:id:kenkoooo:20171201145535p:plain

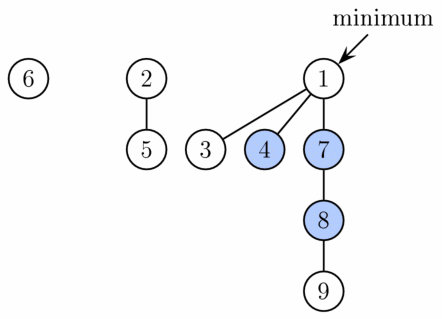
次に、最小値を削除 (pop) することを考えます。先ほど最小値とされていた 1 のノードが削除され、1 を根としたツリーが分解し、新たに 3, 4, 7 をそれぞれ根とした新しいツリーができます。新しいツリーたちはヒープのツリーのリストに入ります。

f:id:kenkoooo:20171201150203p:plain

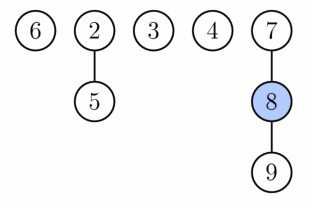
今度はツリーのリストを整理します。ツリーを順番に見ていき、以下の操作を施します。

見ているツリーの根の次数を i とする。

次数 i のツリーとして登録されているツリーが他になければ、今見ているツリーを次数 i のツリーとして登録する。
次数 i のツリーとして登録されているツリーが既にある場合、登録されているツリーの根の値と、今見ているツリーの根の値を比べ、大きい方の根を小さい方の根の下に接続する。この操作で次数 i の根を持ったツリーが 2 つ消え、次数 i+1 を持ったツリーが新たに生成される。

この操作を全て終えると、ヒープ内のツリーの根の次数が全て相異なるようになります。（後述しますが、これは重要なことです）
最後に残っているツリーの根をもう一度全て見て、最小の値を持つ根を最小値として指すようにします。

f:id:kenkoooo:20171201150551p:plain

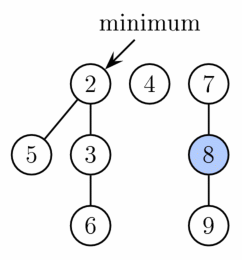
計算量

ツリーのリストを走査するときにノードを参照する回数は、新たに追加されたノードの数 + 最小値のノードの子ノードの数であるが、新たに追加されたノードの数はノードを追加する計算量に含めるとして、最小値のノードの子ノードの数、すなわち最小値のノードの次数が $O(\log n)$ となることを示す。

補題 1

あるノード x について、 x の次数を $x.degree$ と表す。 $x.degree=k$ として、x の k 個の子ノードをそれぞれ $y_1, y_2, y_3, ..., y_k$ として、この順番で x の子として接続されたとする。この時 $y_1.degree \geq 0$ かつ $y_i.degree \geq i - 2 (i=2,3,...,k)$ である。

証明

$y_1.degree \geq 0$ は自明。

$i \geq 2$ に対して $y_i$ を x に接続する時、 $y_1, ... , y_{i-1}$ は既に x の子ノードとして接続されている。つまり $x.degree \geq i-1$ が成り立っている。
ここで $y_i$ が x に子として接続されるためには $x.degree= y_i.degree$ が成り立っていなければならない。よって $y_i.degree \geq i-1$ が成り立つ。
値が減少するバージョンではまだやることがありますが、とりあえずこれで $y_i.degree \geq i-2$ が成り立ったのでこのまま行きます。

補題 2

k 番目のフィボナッチ数を $F_k$ と表す。この時 $F_0=0, F_1=1$ とする。k (k > 2) 番目のフィボナッチ数 $F_k$ の漸化式は $F_k=F_{k-1}+F_{k-2}$ である。

この時、任意の $k \geq 0$ について $F_{k+2} = 1 + \sum^{k}_{i=0} F_i$ が成り立つ。

証明

帰納法で示す。

k=0 のとき成り立つ。

$F_{k+1} = 1 + \sum^{k-1}_{i=0}F_i$ が成り立つことを仮定すると、 $F_{k+2}=F_{k+1}+F_k=F_k+1+ \sum^{k-1}_{i=0}F_i = 1 + \sum^{k}_{i=0} F_i$

補題 3

$\phi$ を $x^2-x-1=0$ の正の解とする。

全ての整数 $k \geq 0$ に対して、 k+2 番目のフィボナッチ数 $F_{k+2}$ は $F_{k+2} \geq \phi^k$ を満たす。

証明

帰納法で示す。

$k=0$ のとき $F_2=1=\phi^0$
$k=1$ のとき $F_3=2>\phi^1$

$F_i + 2 > \phi^i (i=0,1,2,...,k-1)$ を仮定すると $F_{k+2} = F_{k+1} +F_k \geq \phi^{k-1} + \phi^{k-2} = \phi^{k-2}(\phi + 1) = \phi^{k-2} \phi^2 = \phi^k$

補題 4

ノード x について $x.degree=k$ とする。 $size(x)$ を、ノード x を根とする部分木の頂点数とすると、 $size(x) \geq \phi^k$ が成り立つ。

証明

次数 k のあるノード z の $size(z)$ が取りうる最小値を $s_k$ とする。 $s_0=1, s_1=2$ である。また、 $s_k$ は k について単調増加である。z の k 個の子ノードを $y_1, ... , y_k$ とすると、

$size(z) \geq s_k \geq 2 + \sum^{k}_{i=2} s_{y_i.degree} \geq 2 + \sum^{k}_{i=2}s_{i-2}$

(補題 1 より $y_i.degree \geq i-2$ であり、 $s_k$ は単調増加なので $s_{y_i.degree} \geq s_{i-2}$ である)

$s_i \geq F_{i+2} (i=0,1,2,... ,K-1)$ を仮定すると $s_k \geq 2 + \sum^{k}_{i=2}s_{i-2} \geq 2 +\sum^{k}_{i=2}F_{i} = 1 + \sum^{k}_{i=0}F_i = F_{k+2 } \geq \phi^k$

よって $size(x) \geq s_k \geq F_{k+2} \geq \phi^k$

系 5

要素数 n のフィボナッチヒープに属する任意の頂点の最大次数 $D(n)$ は $O(\log n)$ である。

証明

要素数 n のフィボナッチヒープの任意のノードを x とし、 $k = x.degree$ とする。
$n \geq size(x) \geq \phi^k$ だから $\log_{\phi}n \geq k$

よって任意の頂点の次数は $\log_{\phi}n$ で抑えられる。

実装

import java.util.ArrayList;
import java.util.List;

public class LongFibonacciHeap {

  class Node {

    long key = -1;
    int degree = 0;
    Node p = null;
    Node right = null;
    Node left = null;
    List<Node> children = new ArrayList<>();
    boolean mark = false;
  }

  private Node min = null;
  private int size = 0;

  public void insert(Node x) {
    if (min == null) {
      min = x;
      x.right = x;
      x.left = x;
    } else {
      addRoot(x);
      if (x.key < min.key) {
        min = x;
      }
    }
    size++;
  }

  /**
   * Add node x to linked root list
   *
   * @param x node to add
   */
  private void addRoot(Node x) {
    if (min == null) {
      min = x;
      min.right = x;
      min.left = x;
      return;
    }

    Node l = min.left;
    l.right = x;
    min.left = x;

    x.right = min;
    x.left = l;
  }

  /**
   * Remove node x from linked root list
   *
   * @param x node to remove
   */
  private void removeRoot(Node x) {
    Node r = x.right;
    Node l = x.left;
    r.left = l;
    l.right = r;
  }

  /**
   * merge h1 and h2 to generate new one
   *
   * @param h1 heap1 to merge
   * @param h2 heap2 to merge
   * @return merged heap
   */
  public static LongFibonacciHeap unite(LongFibonacciHeap h1, LongFibonacciHeap h2) {
    LongFibonacciHeap h = new LongFibonacciHeap();
    h.min = h1.min;
    if ((h1.min == null) || (h2.min != null && h2.min.key < h1.min.key)) {
      h.min = h2.min;
    }

    // link h1's root list & h2's root list
    if (h1.min != null && h2.min != null) {
      Node n1 = h1.min;
      Node n2 = h2.min;
      Node n1l = n1.left;
      Node n2r = n2.right;

      n1.left = n2;
      n2.right = n1;
      n2r.left = n1l;
      n1l.right = n2r;
    }

    h.size = h1.size + h2.size;
    return h;
  }

  public Node extractMinNode() {
    Node z = min;
    if (z == null) {
      return null;
    }

    for (Node child : z.children) {
      addRoot(child);
      child.p = null;
    }
    removeRoot(z);
    if (z == z.right) {
      min = null;
    } else {
      min = z.right;
      consolidate();
    }
    size--;
    return z;
  }

  public int size() {
    return size;
  }

  private void consolidate() {
    //list up rooted nodes
    ArrayList<Node> rootList = new ArrayList<>();
    rootList.add(min);
    while (rootList.get(rootList.size() - 1).right != rootList.get(0)) {
      Node lastRight = rootList.get(rootList.size() - 1).right;
      rootList.add(lastRight);
    }

    Node[] rootOfDegree = new Node[size + 1];
    for (Node parent : rootList) {
      int d = parent.degree;
      while (rootOfDegree[d] != null) {
        Node child = rootOfDegree[d];
        if (parent.key > child.key) {
          Node t = parent;
          parent = child;
          child = t;
        }
        link(child, parent);
        rootOfDegree[d] = null;
        d++;
      }
      rootOfDegree[d] = parent;
    }

    min = null;
    for (Node node : rootOfDegree) {
      if (node == null) {
        continue;
      }

      if (min == null) {
        node.right = node;
        node.left = node;
        min = node;
      } else {
        addRoot(node);
        if (node.key < min.key) {
          min = node;
        }
      }
    }
  }

  private void link(Node child, Node parent) {
    removeRoot(child);
    parent.degree++;
    parent.children.add(child);
    child.p = parent;
    child.mark = false;
  }

  public void insert(long key) {
    Node x = new Node();
    x.key = key;
    insert(x);
  }
}

フィボナッチヒープを使ってダイクストラやってみた

問題

atcoder.jp

コード

use std::cmp;
use std::collections::HashMap;

const INF: u64 = std::u64::MAX / 2;

fn main() {
    let s = std::io::stdin();
    let mut sc = Scanner { stdin: s.lock() };
    let n: usize = sc.read();
    let m: usize = sc.read();
    let s = sc.read::<usize>() - 1;
    let t = sc.read::<usize>() - 1;

    let mut graph = vec![vec![]; n];
    for _ in 0..m {
        let a = sc.read::<usize>() - 1;
        let b = sc.read::<usize>() - 1;
        let c = sc.read::<u64>();
        graph[a].push((b, c));
        graph[b].push((a, c));
    }

    let dist1 = dijkstra(s, &graph);
    let dist2 = dijkstra(t, &graph);
    for i in 0..n {
        if dist1[i] == dist2[i] && dist1[i] != INF {
            println!("{}", i + 1);
            return;
        }
    }
    println!("-1");
}

fn dijkstra(s: usize, graph: &Vec<Vec<(usize, u64)>>) -> Vec<u64> {
    let n = graph.len();
    let mut dist = vec![INF; n];
    dist[s] = 0;
    let mut heap = FibonacciHeap::new(cmp::min);
    heap.push((0, s));
    while let Some((_, v)) = heap.pop() {
        for &(next, cost) in graph[v].iter() {
            if dist[next] > dist[v] + cost {
                dist[next] = dist[v] + cost;
                heap.push((dist[next], next));
            }
        }
    }
    dist
}

fn store_to_map<T, F>(map: &mut HashMap<usize, Node<T>>, mut node: Node<T>, ordering: F)
where
    T: Copy + PartialEq,
    F: Fn(T, T) -> T,
{
    let d = node.children.len();
    match map.remove(&d) {
        Some(mut other) => {
            let node = if (ordering)(node.key, other.key) == node.key {
                node.children.push(other);
                node
            } else {
                other.children.push(node);
                other
            };
            store_to_map(map, node, ordering);
        }
        None => {
            map.insert(d, node);
        }
    }
}

pub struct FibonacciHeap<T, F> {
    pub nodes: Vec<Node<T>>,
    min_index: usize,
    ordering: F,
}

impl<T, F> FibonacciHeap<T, F>
where
    T: Copy + PartialEq,
    F: Fn(T, T) -> T + Copy,
{
    pub fn new(ordering: F) -> FibonacciHeap<T, F> {
        FibonacciHeap {
            nodes: Vec::new(),
            min_index: 0,
            ordering: ordering,
        }
    }
    pub fn push(&mut self, x: T) {
        let node = Node::new(x);
        self.nodes.push(node);
        let cur_min = self.nodes[self.min_index].key;
        if (self.ordering)(cur_min, x) == x {
            self.min_index = self.nodes.len() - 1;
        }
    }
    pub fn pop(&mut self) -> Option<T> {
        let mut map: HashMap<usize, Node<T>> = HashMap::new();
        let mut popped = None;

        let mut nodes = Vec::new();
        std::mem::swap(&mut self.nodes, &mut nodes);
        for (i, node) in nodes.into_iter().enumerate() {
            if i == self.min_index {
                popped = Some(node.key);
                for node in node.children.into_iter() {
                    store_to_map(&mut map, node, self.ordering);
                }
            } else {
                store_to_map(&mut map, node, self.ordering);
            }
        }

        self.nodes = map.into_iter().map(|(_, node)| node).collect();
        if !self.nodes.is_empty() {
            let mut min = self.nodes[0].key;
            for i in 0..self.nodes.len() {
                if (self.ordering)(min, self.nodes[i].key) == self.nodes[i].key {
                    min = self.nodes[i].key;
                }
            }

            self.min_index = self
                .nodes
                .iter()
                .enumerate()
                .find(|&(_, node)| node.key == min)
                .unwrap()
                .0;
        } else {
            self.min_index = 0;
        }
        popped
    }
}

#[derive(Debug)]
pub struct Node<T> {
    pub key: T,
    pub children: Vec<Node<T>>,
}

impl<T> Node<T> {
    fn new(x: T) -> Node<T> {
        Node {
            key: x,
            children: Vec::new(),
        }
    }
}

pub struct Scanner<R> {
    stdin: R,
}

impl<R: std::io::Read> Scanner<R> {
    pub fn read<T: std::str::FromStr>(&mut self) -> T {
        use std::io::Read;
        let buf = self
            .stdin
            .by_ref()
            .bytes()
            .map(|b| b.unwrap())
            .skip_while(|&b| b == b' ' || b == b'\n')
            .take_while(|&b| b != b' ' && b != b'\n')
            .collect::<Vec<_>>();
        unsafe { std::str::from_utf8_unchecked(&buf) }
            .parse()
            .ok()
            .expect("Parse error.")
    }
    pub fn vec<T: std::str::FromStr>(&mut self, n: usize) -> Vec<T> {
        (0..n).map(|_| self.read()).collect()
    }
    pub fn chars(&mut self) -> Vec<char> {
        self.read::<String>().chars().collect()
    }
}

2017-12-01

リクルートコミュニケーションズを退職しました

その他

adventar.org

豆知識

この記事のタイトルでググると、まともな記事が出てきます。

退職しました

20 ヶ月ほど勤務したリクルートコミュニケーションズ (RCO) を退職しました。RCO ではウェブ広告リアルタイム配信チームで、主に高速化を頑張りました。かなり面白かったです。また、 2 年目に並行して始めた、流通を線形計画問題に落とし込んで解くという仕事も割と面白かったです。

自由な雰囲気で、給料も良く、良い同僚に恵まれもしましたが、若いうちに色んな環境を経験しておきたかったのと、上司いわく「うちは出入り自由なんで」とのことだったので、気楽な気持ちで退職しました。

これが罠で、12月末で退職すれば良かったものを、何故かうっかり 11 月末で退職してしまったがために、12 月のボーナスを貰い損ねてしまいました。さすがに適当に退職し過ぎた・・・

まとめ

積極的な理由がないなら、賞与の後に退職すると良い。

2017-11-06

AOJ 2829 Room Assignment

競技プログラミング AOJ Scala

問題

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2829

解法

JAG の wiki に分かりやすい解説があります。

2017/Practice/模擬国内予選/講評 - ACM-ICPC Japanese Alumni Group

場合分けとしては以下の 3 つです

長さ 3 以上の閉路が存在する場合は 0
閉路を潰した時に、全てのツリーの葉の数が 2 以下でなければ 0
長さ 3 以上の弱連結成分が存在しない時
それ以外

コード

import java.util.Scanner

import scala.collection.mutable.ArrayBuffer

object Main {
  private val Mod = (1e9 + 7).toInt

  // 階乗を前計算しておく
  private val Fact = {
    var cur = 1L
    for (i <- 0 to 200000) yield {
      if (i == 0) {
        1
      } else {
        cur = (cur * i) % Mod
        cur
      }
    }
  }

  // 2 の累乗を前計算しておく
  private val Pow = {
    val pow = new Array[Int](200000)
    pow(0) = 1
    for (i <- 1 until pow.length) pow(i) = pow(i - 1) * 2 % Mod
    pow
  }

  def main(args: Array[String]): Unit = {
    val in = new Scanner(System.in)
    while (true) {
      val n = in.nextInt()
      if (n == 0) {
        return
      }
      val a = for (_ <- 0 until n) yield {
        in.nextInt() - 1
      }
      println(solve(a.toArray))
    }
  }

  // 長さ 3 以上の閉路が存在しないことを確認する
  def cycleCheck(graph: IndexedSeq[Seq[Int]]): Boolean = {
    val cmp = StronglyConnectedComponents.decompose(graph)
    var map = Map[Int, Int]()
    cmp.foreach { c => map += (c -> (map.getOrElse(c, 0) + 1)) }
    map.values.forall(count => count <= 2)
  }

  // 全ての弱連結成分がパスが閉路を潰すとパスになることを確認する
  def pathCheck(graph: IndexedSeq[Seq[Int]]): Boolean = {
    val uf = new UnionFind(graph.size)
    for {
      i <- graph.indices
      j <- graph(i)
    } uf.unite(i, j)

    var map = Map[Int, Int]()
    for {
      i <- graph.indices
      if graph(i).isEmpty
    } {
      val count = map.getOrElse(uf.find(i), 0)
      map += (uf.find(i) -> (count + 1))
    }
    map.values.forall(count => count <= 2)
  }

  // 要素数 2 の弱連結成分の数と、要素数 3 以上の弱連結成分の数を算出する
  def getSize(array: Array[Int]): (Int, Int) = {
    val N = array.length
    val uf = new UnionFind(N)
    for (i <- array.indices) uf.unite(i, array(i))
    val sizes = for {
      i <- 0 until N
      if i == 0 || !uf.isSame(i, 0)
    } yield {
      if (i == 0) {
        uf.partialSizeOf(i)
      } else {
        val s = uf.partialSizeOf(i)
        uf.unite(i, 0)
        s
      }
    }

    var three = 0
    var two = 0
    sizes.foreach(size => if (size == 2) {
      two += 1
    } else {
      three += 1
    })

    (two, three)
  }

  def solve(parent: Array[Int]): Int = {
    val n = parent.length
    val combination = new Combination(n + 1, Mod)

    val graph = parent.indices.map(i => new ArrayBuffer[Int]())
    parent.indices.foreach(i => graph(parent(i)).append(i))

    if (cycleCheck(graph) && pathCheck(graph)) {
      val (two, three) = getSize(parent)
      if (three == 0) {
        // 長さ 3 以上の弱連結成分が存在しないとき
        var cur: Long = ((two + 2) / 2) % Mod
        cur = cur * Pow(two) % Mod
        cur = cur * Fact(two) % Mod
        cur.toInt
      } else {
        var ans = 0L
        for (i <- 0 to math.min(two + three - 2, two)) {
          var cur = combination.get(two + three - i - 2, two - i).toLong
          cur = cur * Fact(two) % Mod
          cur = cur * Fact(three) % Mod
          cur = cur * Pow(two + three) % Mod
          cur = cur * (two + three - i - 1) % Mod
          cur = cur * ((i + 2) / 2) % Mod
          ans = (ans + cur) % Mod
        }
        for (i <- 0 to math.min(two + three - 1, two)) {
          var cur = combination.get(two + three - i - 1, two - i).toLong
          cur = cur * Fact(two) % Mod
          cur = cur * Fact(three) % Mod
          cur = cur * Pow(two + three) % Mod
          cur = cur * ((i + 2) / 2) % Mod
          ans = (ans + cur * 2) % Mod
        }
        ans.toInt
      }
    } else {
      0
    }
  }

  class UnionFind(n: Int) {
    private val parent = (0 until n).toArray
    private val sizes = Array.fill[Int](n)(1)
    private var _size = n

    def find(x: Int): Int = {
      if (x == parent(x)) {
        x
      } else {
        parent(x) = find(parent(x))
        parent(x)
      }
    }

    def unite(a: Int, b: Int): Boolean = {
      val fa = find(a)
      val fb = find(b)
      if (fa == fb) {
        false
      } else {
        val (x, y) = if (sizes(fa) >= sizes(fb)) {
          (fa, fb)
        } else {
          (fb, fa)
        }

        parent(y) = x
        sizes(x) += sizes(y)
        sizes(y) = 0

        _size -= 1
        true
      }
    }

    def isSame(x: Int, y: Int): Boolean = find(x) == find(y)

    def partialSizeOf(x: Int): Int = sizes(find(x))

    def size(): Int = _size
  }

  class Combination(max: Int, mod: Int) {
    private val inv = new Array[Long](max + 1)
    private val fact = new Array[Long](max + 1)
    private val invFact = new Array[Long](max + 1)
    inv(1) = 1
    for (i <- 2 to max) inv(i) = inv(mod % i) * (mod - mod / i) % mod
    fact(0) = 1
    invFact(0) = 1
    for (i <- 1 to max) fact(i) = (fact(i - 1) * i) % mod
    for (i <- 1 to max) invFact(i) = (invFact(i - 1) * inv(i)) % mod

    /**
      * get nCm
      */
    def get(n: Int, m: Int): Int = {
      if (n < m) {
        0
      } else fact(n) * invFact(m) % mod * invFact(n - m) % mod
    }.toInt
  }

  object StronglyConnectedComponents {
    def decompose(graph: IndexedSeq[Seq[Int]]): Array[Int] = {
      val vs = new ArrayBuffer[Int]()
      val V = graph.size
      val cmp = new Array[Int](V)

      val rg = graph.indices.map(_ => new ArrayBuffer[Int]())
      for {
        from <- graph.indices
        to <- graph(from)
      } rg(to).append(from)

      var used = Array.fill[Boolean](V)(false)
      var stack = List[Int]()
      val added = Array.fill[Boolean](V)(false)
      for {
        i <- used.indices
        if !used(i)
      } {
        stack = i :: stack
        while (stack.nonEmpty) {
          val v = stack.head
          used(v) = true
          var pushed = false
          for {
            u <- graph(v).reverse
            if !used(u)
          } {
            stack = u :: stack
            pushed = true
          }
          if (!pushed) {
            stack = stack.tail
            if (!added(v)) {
              vs.append(v)
              added(v) = true
            }
          }
        }
      }

      used = Array.fill[Boolean](V)(false)
      var k = 0
      for {
        i <- vs.reverse
        if !used(i)
      } {
        stack = i :: stack
        used(i) = true
        cmp(i) = k
        while (stack.nonEmpty) {
          val v = stack.head
          var pushed = false
          for {
            u <- rg(v)
            if !used(u)
          } {
            used(u) = true
            cmp(u) = k
            stack = u :: stack
            pushed = true
          }
          if (!pushed) {
            stack = stack.tail
          }
        }
        k += 1
      }
      cmp
    }
  }

}

2017-11-01

AOJ 3019 Picnic

Scala 競技プログラミング AOJ

問題

Picnic | Aizu Online Judge

解法

ワーシャルフロイド→巡回セールスマン→半分全列挙→個数制約付きナップサック

コード

import java.util

import scala.io.StdIn
import scala.util.Try

object Main extends App {
  val INF: Long = 1e15.toLong
  val (n, x, y) = {
    val in = StdIn.readLine().split(" ").map(_.toInt)
    (in(0), in(1), in(2))
  }
  val sweets = for (_ <- 0 until n) yield {
    val k = StdIn.readLine().toInt
    for (_ <- 0 until k) yield {
      val in = StdIn.readLine().split(" ").map(_.toInt)
      Sweet(in(0), in(1), in(2))
    }
  }

  val dist = for (_ <- 0 until n) yield StdIn.readLine().split(" ").map(_.toLong)
  for (k <- 0 until n) for (i <- 0 until n) for (j <- 0 until n) dist(i)(j) = math.min(dist(i)(j), dist(i)(k) + dist(k)(j))

  val cost = Array.fill[Long](1 << n, n)(INF)
  cost(0)(0) = 0
  for (mask <- 0 until 1 << n)
    for (cur <- 0 until n)
      for (next <- 0 until n)
        if ((mask & (1 << next)) == 0) {
          val add = dist(cur)(next)
          cost(mask | (1 << next))(next) = math.min(cost(mask | (1 << next))(next), cost(mask)(cur) + add)
        }


  def knapsack(dp: Array[Long], available: Seq[Sweet]): Unit = {
    for {
      sweet <- available
      money <- 0 until sweet.price
    } {
      val deque = new util.ArrayDeque[(Int, Long)]()
      var num = 0
      while (num * sweet.price + money <= y) {
        val next = num * sweet.price + money


        val v = dp(next) - num * sweet.value
        while (!deque.isEmpty && deque.peekLast()._2 <= v) deque.pollLast()
        deque.addLast((num, v))

        dp(next) = deque.peekFirst()._2 + num * sweet.value
        if (deque.peekFirst()._1 == num - sweet.remain) deque.pollFirst()

        num += 1
      }
    }
    for (i <- 1 until dp.length) dp(i) = math.max(dp(i), dp(i - 1))
  }


  val prefix = n / 2
  val suffix = n - prefix

  val prefixDp = Array.fill[Long](1 << prefix, y + 1)(0)
  for (prefixMask <- 0 until 1 << prefix) {
    val mask = prefixMask << suffix
    val dp = prefixDp(prefixMask)
    val available = for {
      i <- 0 until n
      if (mask & (1 << i)) != 0
      sweet <- sweets(i)
    } yield sweet
    knapsack(dp, available)
  }

  val suffixDp = Array.fill[Long](1 << suffix, y + 1)(0)
  for (mask <- 0 until 1 << suffix) {
    val dp = suffixDp(mask)
    val available = for {
      i <- 0 until n
      if (mask & (1 << i)) != 0
      sweet <- sweets(i)
    } yield sweet
    knapsack(dp, available)
  }
  var ans = 0L
  for (mask <- 0 until 1 << n) {
    val suffixMask = mask & ((1 << suffix) - 1)
    val prefixMask = mask >> suffix
    val travelingCost = (for (last <- 0 until n) yield {
      cost(mask)(last) + dist(last)(0)
    }).min
    val money = math.min(x - travelingCost, y).toInt
    for (prefixMoney <- 0 to money) {
      val suffixMoney = money - prefixMoney
      val value = prefixDp(prefixMask)(prefixMoney) + suffixDp(suffixMask)(suffixMoney)
      ans = math.max(ans, value)
    }
  }
  println(ans)
}

case class Sweet(price: Int, value: Int, remain: Int)

2017-09-27

AIM Tech Round 4 (Div. 1) D. Dynamic Shortest Path

Codeforces Rust 競技プログラミング

問題

http://codeforces.com/contest/843/problem/D

解法

最初にダイクストラで距離を求めておき、各クエリごとにダイクストラで追加で増えた分の距離を計算して加算していく。各クエリごとに距離は 1 しか増えないので、キューを距離の数だけ用意すれば、クエリごとのダイクストラの計算量は $O(V+E)$ になる。

よって、最初のダイクストラが $O( (V+E)log V)$ クエリごとのダイクストラが全部で $O(Q (V+E) )$ となるので、全体で $O( (V+E)(Q+\log V) )$ で $Q=2000, E = 10^5$ とかなので、 10 秒あれば間に合う（いいえ）。

コード

use std::io;
use std::str;
use std::usize;
use std::collections::BinaryHeap;
use std::cmp::Ordering;
use std::collections::BTreeMap;
use std::collections::VecDeque;
use std::cmp;

static INF: i64 = 1 << 60;
static MAX_REQ: usize = 2000000;

fn main() {
    let start = 0;
    let (n, m, q) = {
        let v = read_values::<usize>();
        (v[0], v[1], v[2])
    };

    let mut graph: Vec<Vec<Edge>> = vec![Vec::new(); n];
    let mut edges = Vec::new();
    for _ in 0..m {
        let (from, to, cost) = {
            let v = read_values::<usize>();
            (v[0] - 1, v[1] - 1, v[2] as i64)
        };
        edges.push((from, graph[from].len()));
        graph[from].push(Edge { to: to, cost: cost });
    }

    let mut shortest_dist = dijkstra(start, &graph);
    let mut deque = vec![VecDeque::new(); MAX_REQ];
    let mut add = vec![INF; n];

    let mut modify_queries = Vec::new();

    for _ in 0..q {
        let queries = read_values::<usize>();
        if queries[0] == 1 {
            let to = queries[1] - 1;
            let num = modify_queries.len();

            for edge_idx in &modify_queries {
                let (from, idx): (usize, usize) = edges[*edge_idx];
                unsafe { graph[from].get_unchecked_mut(idx).cost += 1; }
            }
            modify_queries.clear();

            add[start] = 0;
            deque[0].push_back(start);

            for dist in 0..(num + 1) {
                while !deque[dist].is_empty() {
                    let cur = deque[dist].pop_front().unwrap();
                    if add[cur] != dist as i64 {
                        continue;
                    }
                    for e in &graph[cur] {
                        let d = shortest_dist[cur] + add[cur] - shortest_dist[e.to] + e.cost;
                        if d as usize <= num && add[e.to] > d {
                            add[e.to] = d;
                            deque[d as usize].push_back(e.to);
                        }
                    }
                }
            }

            for i in 0..n {
                shortest_dist[i] = cmp::min(shortest_dist[i] + add[i], INF);
                add[i] = INF;
            }

            if shortest_dist[to] >= INF {
                println!("-1");
            } else {
                println!("{}", shortest_dist[to]);
            }
        } else {
            let num = queries[1];
            for i in 0..num { modify_queries.push(queries[i + 2] - 1); }
        }
    }
}

fn dijkstra(start: usize, graph: &Vec<Vec<Edge>>) -> Vec<i64> {
    let n = graph.len();
    let mut heap = BinaryHeap::<Edge>::new();
    heap.push(Edge { to: start, cost: 0 });
    let mut dist = vec![INF; n];
    dist[start] = 0;
    while !heap.is_empty() {
        let p: Edge = heap.pop().unwrap();
        for e in &graph[p.to] {
            if dist[e.to] > e.cost + dist[p.to] {
                dist[e.to] = e.cost + dist[p.to];
                heap.push(Edge { to: e.to, cost: dist[e.to] });
            }
        }
    }
    dist
}

#[derive(Copy, Clone, Eq, PartialEq)]
struct Edge {
    to: usize,
    cost: i64,
}

impl Ord for Edge {
    fn cmp(&self, other: &Edge) -> Ordering {
        other.cost.cmp(&self.cost)
    }
}

impl PartialOrd for Edge {
    fn partial_cmp(&self, other: &Edge) -> Option<Ordering> {
        Some(self.cmp(other))
    }
}

fn read_line() -> String {
    let stdin = io::stdin();
    let mut buf = String::new();
    stdin.read_line(&mut buf).unwrap();
    buf
}

fn read_values<T>() -> Vec<T>
    where T: std::str::FromStr,
          T::Err: std::fmt::Debug
{
    read_line()
        .split(' ')
        .map(|a| a.trim().parse().unwrap())
        .collect()
}

2017-09-27

会津合宿 2017 2 日目 G : Picnic

AOJ Scala 競技プログラミング

問題

http://judge.u-aizu.ac.jp/onlinejudge/cdescription.jsp?cid=ACPC2017Day2&pid=G

解法

ワーシャルフロイドと巡回セールスマン問題の bit DP で、ある町の部分集合を回って戻ってくるのにかかるコストを前計算しておく。

さらに、町の集合を $A_1, A_2$ の 2 つに分け、各集合のうちの部分集合を回った時に得られる幸福度を、個数制約付きナップサック問題をといて求める。

すると、 $A_1$ の部分集合と $A_2$ の部分集合を組み合わせることで、ある部分集合の最大値を求めることができる。

コード

import java.util.Scanner

object Main {
  def main(args: Array[String]): Unit = {
    val in = new Scanner(System.in)
    val N = in.nextInt()
    val X = in.nextInt()
    val Y = in.nextInt()
    val foods = (for (_ <- 0 until N) yield {
      val K = in.nextInt()
      (for (_ <- 0 until K) yield {
        val a = in.nextInt()
        val b = in.nextInt()
        val c = in.nextInt()
        (a, b, c)
      }).toArray
    }).toArray

    val dist = (for (_ <- 0 until N) yield (for (_ <- 0 until N) yield in.nextInt()).toArray).toArray
    for {
      k <- 0 until N
      i <- 0 until N
      j <- 0 until N
    } dist(i)(j) = math.min(dist(i)(j), dist(i)(k) + dist(k)(j))

    val cost = Array.fill(1 << (N + 1), N + 1)(Int.MaxValue / 2)
    cost(1)(0) = 0
    for {
      mask <- 0 until (1 << N)
      current <- 0 until N
      next <- 1 until (N + 1)
      if (mask & (1 << current)) != 0
      if (mask & (1 << next)) == 0
    } {
      val nextMask = mask | (1 << next)
      cost(nextMask)(next) = math.min(cost(nextMask)(next), cost(mask)(current) + dist(current)(next % N))
    }

    val bottom = N / 2
    val top = N - bottom

    val deq = new Array[Int](1000000)
    val deqv = new Array[Int](1000000)

    def knapsack(mask: Int, dp: Array[Int]): Unit = {
      dp(0) = 0
      for {
        i <- 0 until N
        if (mask & (1 << i)) != 0
        (price, value, remain) <- foods(i)
        a <- 0 until price
      } {
        var s = 0
        var t = 0

        var num = 0
        while (num * price <= (Y - a)) {
          val v = dp(num * price + a) - num * value
          while (s < t && deqv(t - 1) <= v) {
            t -= 1
          }
          deq(t) = num
          deqv(t) = v
          t += 1

          dp(num * price + a) = deqv(s) + num * value
          if (deq(s) == num - remain) {
            s += 1
          }

          num += 1
        }
      }

      for {
        i <- 1 to Y
      } {
        dp(i) = math.max(dp(i), dp(i - 1))
      }
    }

    val bottomDp = Array.fill[Int](1 << bottom, Y + 1)(-1)
    val topDp = Array.fill[Int](1 << top, Y + 1)(-1)
    for (mask <- 0 until (1 << bottom)) {
      knapsack(mask, bottomDp(mask))
    }
    for (mask <- 0 until (1 << top)) {
      knapsack(mask << bottom, topDp(mask))
    }

    var max = 0
    for {
      mask <- 0 until (1 << N)
    } {
      val moveCost = cost(mask | (1 << N))(N)
      val budget = math.min(Y, X - moveCost)
      val bottomMask = mask & ((1 << bottom) - 1)
      val topMask = mask >> bottom

      if (budget > 0) {
        for {
          bottomBudget <- 0 to budget
        } {
          max = math.max(max, bottomDp(bottomMask)(bottomBudget) + topDp(topMask)(budget - bottomBudget))
        }
      }
    }
    println(max)
  }
}

2017-09-20

会津合宿 2017 3 日目 E : Taiyaki-Master and Eater

AOJ 競技プログラミング Scala

問題

AIZU ONLINE JUDGE

解法

2次元のBITを貼る。

コード

import java.util.Scanner

import scala.collection.mutable.ArrayBuffer

object Main extends App {
  val in = new Scanner(System.in)
  val H = in.nextInt()
  val W = in.nextInt()
  val T = in.nextInt()
  val Q = in.nextInt()

  var queries = new ArrayBuffer[(Int, Int, Int, Int, Int, Int)]()
  for (_ <- 0 until Q) {
    val t = in.nextInt()
    val c = in.nextInt()
    val h = in.nextInt()
    val w = in.nextInt()
    val (h2, w2) = if (c == 2) {
      (in.nextInt(), in.nextInt())
    } else {
      (0, 0)
    }
    queries.append((t, c, h, w, h2, w2))
    if (c == 0) {
      // 焼き上がり
      queries.append((t + T, -1, h, w, h2, w2))
    }
  }
  queries = queries.sortBy(q => (q._1, q._2))

  val f1 = new Fenwick2D(H, W)
  val f2 = new Fenwick2D(H, W)
  queries.foreach { case (_, c, h, w, h2, w2) =>
    c match {
      case -1 =>
        // 1->2
        if (f1.get(h, w) != 0) {
          f1.update(h, w, 0)
          f2.update(h, w, 1)
        }
      case 0 =>
        // 0->1
        f1.update(h, w, 1)
      case 1 =>
        // 2->0
        f2.update(h, w, 0)
      case 2 =>
        // count
        val a = f2.sum(h, w, h2, w2)
        val b = f1.sum(h, w, h2, w2)
        println(s"$a $b")
    }
  }


}

/**
  * 1-indexed 2-dimensional Fenwick's tree
  *
  * @param h height
  * @param w width
  */
class Fenwick2D(h: Int, w: Int) {
  val N: Int = h + 1
  val M: Int = w + 1
  val data: Array[Array[Long]] = Array.fill[Long](N + 1, M + 1)(0)

  def add(x: Int, y: Int, v: Long): Unit = {
    var i = x
    while (i <= N) {
      var j = y
      while (j <= M) {
        data(i)(j) += v
        j += j & -j
      }
      i += i & -i
    }
  }

  def update(x: Int, y: Int, v: Long): Unit = add(x, y, v - sum(x, y, x, y))

  def get(x: Int, y: Int): Long = sum(x, y, x, y)

  def sum(x0: Int, y0: Int, x1: Int, y1: Int): Long = {

    def partialSum(x: Int, y: Int): Long = {
      var res = 0L
      var i = x
      while (i > 0) {
        var j = y
        while (j > 0) {
          res += data(i)(j)
          j -= j & -j
        }
        i -= i & -i
      }
      res
    }

    partialSum(x1, y1) - partialSum(x0 - 1, y1) - partialSum(x1, y0 - 1) + partialSum(x0 - 1, y0 - 1)
  }


}